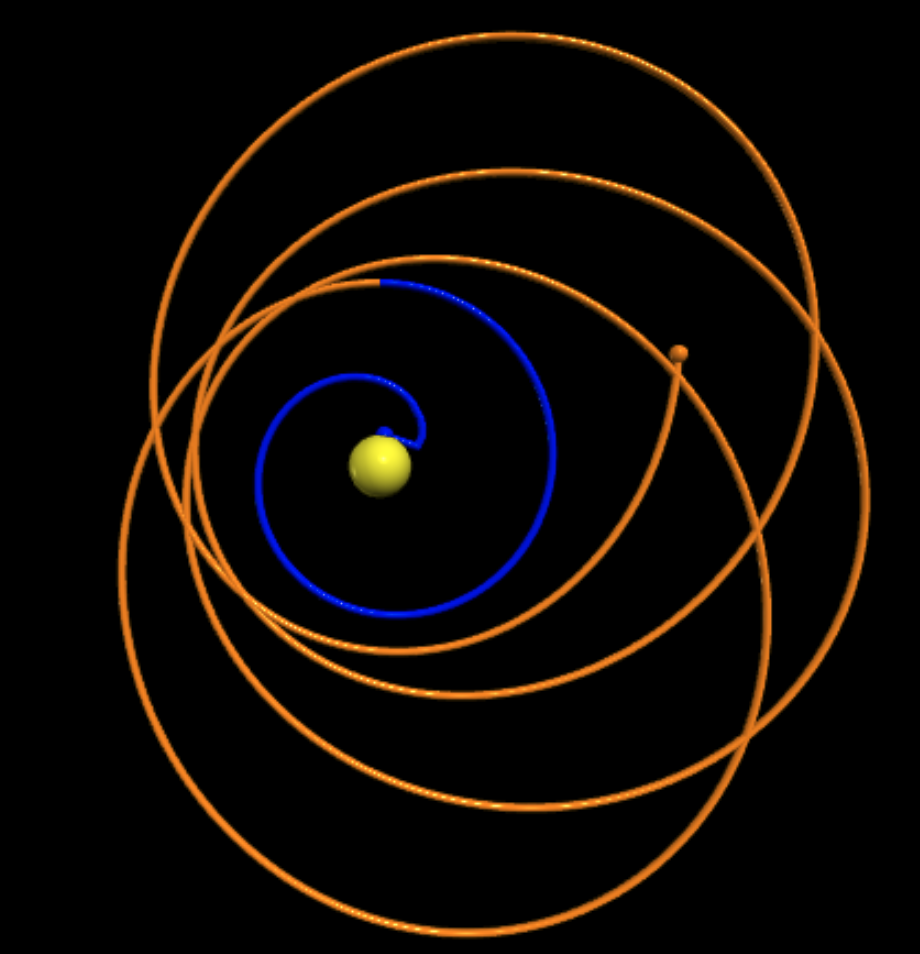
Orbits Around a Spinning Black Hole

This simulation tracks two particles as they orbit in opposite directions around a spinning black hole.

• Both particles start at the same initial position and speed, yet the orbits evolve quite differently! Can you guess the direction of black hole spin?
• Turn the black hole spin off for comparison. (You can turn the spin on/off even while the particles are moving, but for the cleanest comparison, click either slider to return to the same initial conditions.)
• Try giving the particles zero initial speed. Intuition says they should drop straight in, but what happens when the black hole spin is on? Also try giving them a small speed (such as 0.1) to differentiate between the two particles.
• The speed slider is in units of the Newtonian escape speed. If gravity were Newtonian, the default value of 0.71 (actually 1/√2) would yields perfectly circular orbits. Even with black hole spin off, you can see that an orbit of this speed is non-Newtonian.

• The simulation gets very coarse near the Schwarzschild radius. We stop tracking any particle that hits this radius. (Black belts will know that this radius is not the same as the event horizon when the black hole is spinning, but the simulation uses this simple criterion rather than checking for event horizons.)
• We make no attempt to simulate what a distant observer sees. The simulation takes steps in proper time, so a particle can reach the Schwarzschild radius in finite time.
• We simulate only orbits in the equatorial plane. Orbits that depart from this plane exhibit interesting complications beyond the scope of this project. I can recommend this document for more details (see page 20 for example).
• Some of the calculation steps use approximations, but these shortcuts don't change the qualitative behavior.

Click on the image to start.