Click on the image to begin.
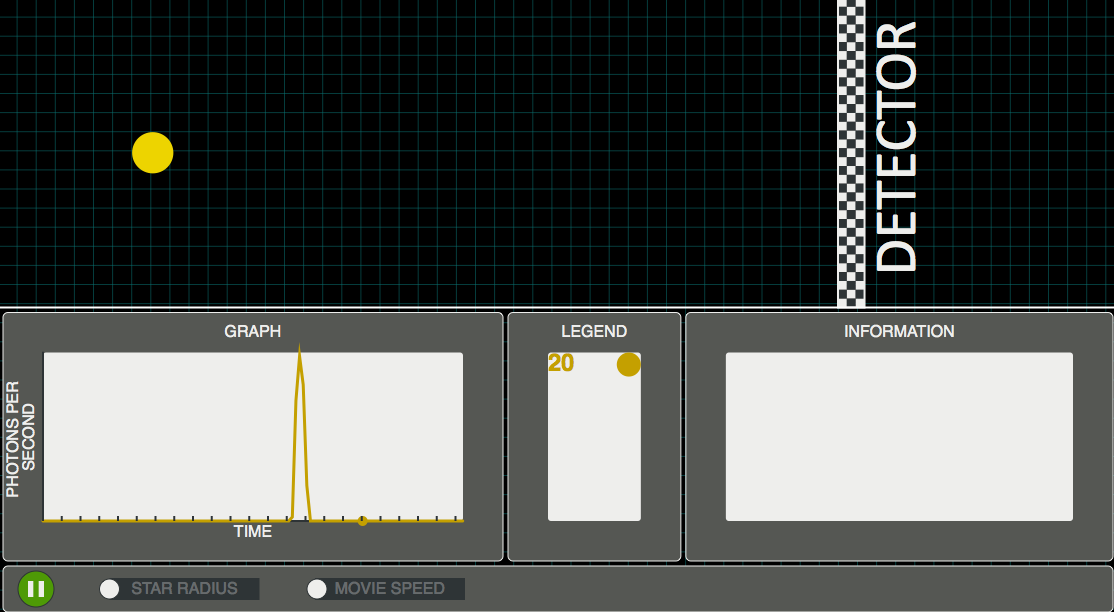
How do we know something is a compact object when even a large star is much smaller than the angular resolution of our telescopes? There is a basic, powerful argument, but until now no one has produced a really good visualization of it. The argument is: if the object were to suddenly give off a flash of light (from all points on its surface), we wouldn't see an instantaneous flash of light because we would first see the light only from the nearest tip of the object. After seeing that first bit of light, we have to wait for some extra time, corresponding to the light-travel time across the object, before we see the last bit of the "instantaneous flash." Therefore we observe the flash to have a duration which is equal to the object's size divided by the speed of light.

This animation created by Alejandro Angulo, Taylor Goolsby, and Rudy Huezo, lets you change the size of the object and see how the light from an instantaneous flash is spread out across the "finish line" which in practice would be a telescope. You can also move the finish line closer or further from the object and see that the object's distance is irrelevant to the timing argument. You can overlay the light curves—the graphs of intensity vs time—for up to seven objects of different sizes. You can also slow down the speed of the light if you want to see in detail how their crossing of the finish line is related to the light curve. Note that the movie speed starts at zero so you can gradually increase it to your liking.
In real life, objects don't give off instantaneous flashes, but their luminosity changes over some period of time. How do we disentangle this from the light travel time effect? Assuming that the luminosity changed instantaneously causes us to overestimate the size of the object (something can take years to vary even it it's much smaller across than a light year). But we're actually ok with that because we use this argument to make statements such as "this object is so small that it must be an accretion disk around a black hole." If we overestimate the size of the object, we will err on the side of caution when deciding if an object is so small that it must be a black hole. In other contexts, overestimation may not be ok, but in this context it just means we are being cautious. Another way to say this is that the variability timing argument gives us an upper limit on the size of the object.
|
Another common question is whether the light travel time gives us the diameter of the object, the radius of the object, or something else. The answer: it depends. If you believe that, as in the simulation, light from the back side of the object can reach us (perhaps because the accretion disk is tilted with respect to our line of sight), then it's the diameter. If the object is an opaque sphere, we can only see the front side so we should think in terms of the radius. We can't know these things for sure, so we build models and ask how well they match the data. For example, the opaque sphere model and the tilted accretion disk model predict very different shapes for the light curves (convince yourself that the opaque sphere should cut off rather suddenly compared to its onset). Professional astronomers spend a great deal of time building sophisticated models. For example, taking the NASA artist's conception of an accreting binary system at right as our model, we could generate quite detailed predictions for the light curve as the members orbit each other and take turns blocking each other's light. The level of detail of these predictions would extend to predictions of how the light curve is different when looking at different colors of light. Introductory astronomy students won't be doing this kind of detailed modeling, but they should understand the principles which guide the modeling. So, for example, students should understand that if the object has a hot spot that varies then the variability timing argument may reveal the size of the hot spot rather than the size of the whole object. | 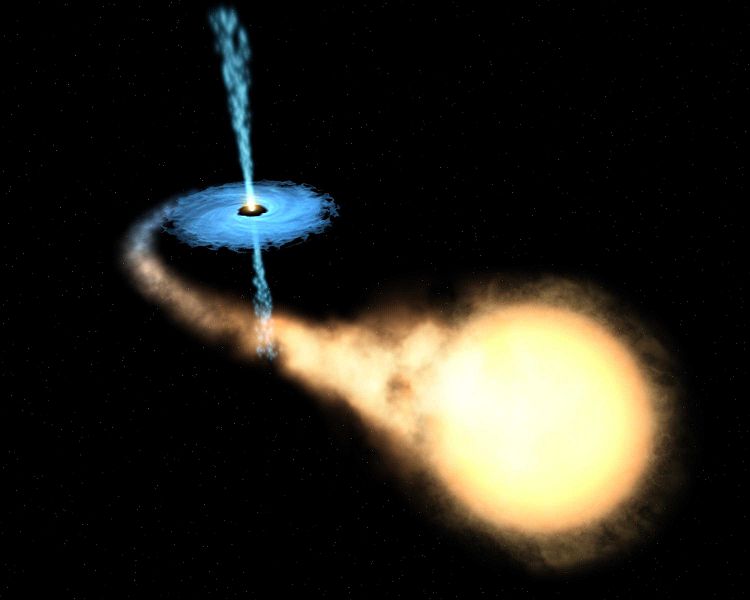 |